Didaktická prostředí

AUTOBUS – porozumím číslům vyjadřujícím změnu stavu. Lépe se orientuji v souboru dat, který obsahuje jak stavy, tak změny a porovnání.

BAREVNÉ TROJICE – rozvíjím své řešitelské strategie aritmetických úloh (např. dramatizace, simulovaná dramatizace) obohacených o parametr barvy.
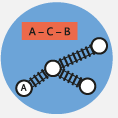
CYKLOTRASY A VLAKOVÉ LINKY – propojuji algebraickou a geometrickou situaci. Systematicky prohledávám všechny možnosti, odhaluji nové vztahy vyvozené ze vztahů původních.

DŘÍVKA – poznávám rovinnou geometrii manipulativní činností. Tvořím a přeměňuji tvary podle daných podmínek. Získávám zkušenosti s obsahem, obvodem, jednoduchými zlomky a posloupnostmi.

GEODESKA – hlouběji poznávám „malé“ mnohoúhelníky. Hledám tvary splňující dané podmínky, pracuji s obvodem a obsahem různých tvarů.
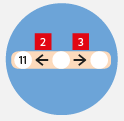
HADI – poznávám vazby souboru čísel, která vystupují jak v roli vztahu, tak v roli operátora. Zobecňuji konkrétní poznatky. Rozvíjím schopnost řešit soustavu rovnic metodou pokus omyl.

HÁZENÍ KOSTKOU – získávám zkušenosti s náhodnými jevy. Porozumím zákonitostem v oblasti pravděpodobnosti a práce se statistickými soubory. Budu odolnější proti hazardu.
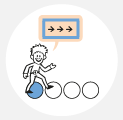
KROKOVÁNÍ A SCHODY – porozumím číslům vyjadřujícím změnu polohy nebo porovnání poloh. Otevřu si svět záporných čísel, později porozumím práci se znaménky. Učím se písemně zaznamenat proces.
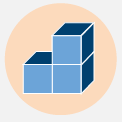
KRYCHLOVÉ STAVBY – poznávám prostorovou geometrii manipulativní činností. Tvořím a přeměňuji stavby podle daných podmínek. Zapisuji stavby a proces jejich přetváření různými jazyky. Rozvíjím svou schopnost překládat z jednoho jazyka do druhého.
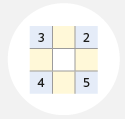
NÁSOBILKOVÉ ČTVERCE – procvičuji násobilku v grafickém prostředí, které mi časem po rozšíření umožní odhalovat vztahy mezi čtyřmi základními operacemi.

NEPOSEDOVÉ – rozvíjím svou schopnost rekonstruovat narušenou číselnou strukturu v prostředí běžných vztahů, v prostředí součtových trojúhelníků nebo hadů.

OBLÉKÁNÍ KRYCHLE – sbírám zkušenosti k poznávání pojmu „síť krychle“. Manipulativně propojuji 2D a 3D geometrii. Rozvíjím si prostorovou představivost.
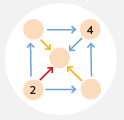
PAVUČINY – pracuji v prostředí podobném hadům rozšířeném o geometricky bohatší zápis doplněný parametrem barvy. Poznávám číselné vztahy, které se časem rozšíří o vztahy parametrické a později
i algebraické.

RODOKMEN – zdokonaluji svou schopnost přesného vyjadřování. Získávám zkušenosti s relacemi a jejich skládáním, propojenými s úlohami o věku.
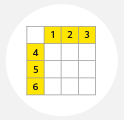
SOUČTOVÉ TABULKY – procvičuji sčítání a odčítání, hledám a objevuji různé vazby mezi čísly ve struktuře tabulky.

SOUČTOVÉ TROJÚHELNÍKY – poznávám bohatší soubor geometricky popsaných aritmetických vztahů. Rozvíjím schopnost řešit soustavu rovnic metodou pokus omyl. Objevuji zákonitosti jako cesty k urychlení řešení úloh.
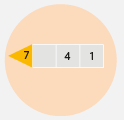
SOUSEDÉ – získávám zkušenosti se základní vazbou aritmetiky, vztahem mezi sčítáním, součtem, odčítáním a rozdílem. Objevuji nové číselné zákonitosti.
VÝSTAVIŠTĚ – orientuji se v prostředí, které vzájemně propojuje geometrii a číselnou řadu. Rozvíjím schopnost rozhodovat a promýšlet několik kroků dopředu.

ZVÍŘÁTKA DĚDY LESONĚ – pracuji s veličinou zapsanou ikonicky, nikoli číslem. Získávám zkušenosti s náročnějšími myšlenkami, které použiji při poznávání rovnic.
HRA SOVA – propojuji oblast logického (kauzálního) myšlení a oblast, z níž je galerie hledaných objektů. Např.
rovinné nebo prostorové geometrie, čísel, objektů běžného života.
PARKETY – získávám zkušenosti s analýzou a syntézou skupiny rovinných tvarů, z nichž některé mohou být
obohaceny o číselné údaje.
SLOVNÍ ÚLOHY – zvyšuji svou schopnost modelovat slovní popis situace nebo procesu dramatizací, simulovanou dramatizací, manipulací, obrázkem, grafem, tabulkou nebo souborem číselných vztahů. Poznávám úlohy s větším počtem řešení. Získávám zkušenosti s úlohami s parametrem a s antisignálem. Dokážu se podílet na tvorbě slovních úloh, a využívat tak své znalosti i kompetence.

Nabídka sekce: O metodě
